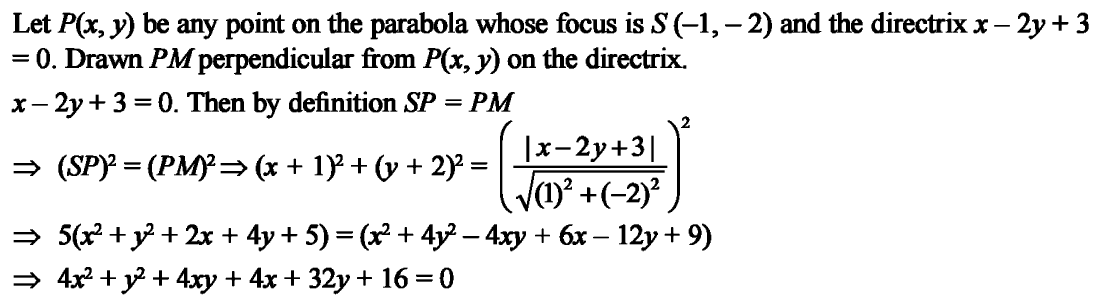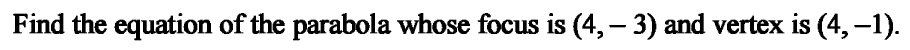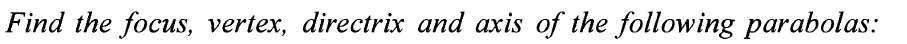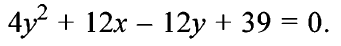PARABOLA(HOTS,BOARD LEVEL)

Example 1

1. Find the vertex, focus, directrix, axis and latusrectum of the parabola y\(^{2}\) - 4x - 4y = 0

The given equation of the parabola is y\(^{2}\) - 4x - 4y = 0

⇒ y\(^{2}\) - 4y = 4x

⇒ y\(^{2}\) - 4y + 4 = 4x + 4, (Adding 4 on both sides)

⇒ (y - 2)\(^{2}\) = 4(x  + 1) ……………………………….. (i)

Shifting the origin to the point (-1, 2) without rotating the axes and denoting the new coordinates with respect to these axes by X and Y, we have

x = X + (-1), y = Y + 2 ……………………………….. (ii)

Using these relations equation (i), reduces to

Y\(^{2}\) = 4X……………………………….. (iii)

This is of the form Y\(^{2}\) = 4aX. On comparing, we get 4a = 4 ⇒ a = 1.

The coordinates of the vertex with respect to new axes are (X = 0, Y = 0)

So, coordinates of the vertex with respect to old axes are (-1, 2), [Putting X= 0, Y = 0 in (ii)].

The coordinates of the focus with respect to new axes are (X = 1, Y = 0)

So, coordinates of the focus with respect to old axes are (0, 2), [Putting X= 1, Y = 0 in (ii)].

Equation of the directrix of the parabola with respect to new axes in X = -1

So, equation of the directrix of the parabola with respect to old asex is x = -2, [Putting X = -1, in (ii)].

Equation of the axis of the parabola with respect to new axes is Y = 0.

So, equation of axis with respect to old axes is y = 2, [Putting Y = 0, in (ii)].

Example 2

2. Write the parametric equation of the parabola (x + 2)\(^{2}\) = - 4(y + 1).

Solution:

The given equation of the parabola is (x + 2)\(^{2}\) = - 4(y + 1).

Then parametric equation of the parabola (x + 2)\(^{2}\) = - 4(y + 1) are

x + 2 = 2t and y + 1 = -t\(^{2}\)

⇒ x = 2t – 2 and y = -t\(^{2}\) – 1.

Example 3

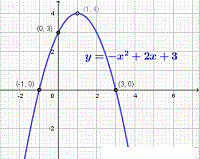
Find the x and y intercepts, the vertex and the axis of symmetry of the parabola with equation y = - x 2 + 2 x + 3?


The x intercepts are the intersection of the parabola with the x axis which are points on the x axis and therefore their y coordinates are equal to 0. Hence we need to solve the equation:
0 = - x 2 + 2 x + 3
Factor right side of the equation: -(x - 3)(x + 1)() = 0
x intercepts are: Solve for x: x = 3 and x = -1 ,
The y intercepts is the intersection of the parabola with the y axis which is a points on the y axis and therefore its x coordinates are equal to 0
y intercept is : y = - (0)2 + 2 (0) + 3 = 3 ,
The vertex is found by writing the equation of the parabola in vertex form y = a(x - h) 2 + k and identifying the coordinates of the vertex h and k.
y = - x 2 + 2 x + 3 = -( x 2 - 2 x - 3) = -( (x - 1) 2 - 1 - 3) = -(x - 1) 2 + 4
Vertex at the point (1 , 4)
You may verify all the above points found using the graph of y = - x 2 + 2 x + 3 shown below.

x and y intercepts of parabola


Example 4

What are the points of intersection of the line with equation 2x + 3y = 7 and the parabola with equation y = - 2 x 2 + 2 x + 5?

The points of intersection of the two parabolas are solutions to the simultaneous equations y = -(x - 3) 2 + 2 and y = x 2 - 4x + 1.
-(x - 3) 2 + 2 = x 2 - 4x + 1
-2x 2 + 10 x - 8 = 0
-x 2 + 5 x - 4 = 0
Solutions: x = 1 and x = 4
Use one of the equations to find y:
x = 1 in the equation y = -(x - 3) 2 + 2 to obtain y = -(1 - 3) 2 + 2 = -2
x = 4 in the equation y = -(x - 3) 2 + 2 to obtain y = -(4 - 3) 2 + 2 = 1
Points: (1 , -2) and (4 , 1)

Example 5

Find the points of intersection of the two parabolas with equation y = -(x - 3) 2 + 2 and y = x 2 - 4x + 1.

  • Solution
    The points of intersection of the two parabolas are solutions to the simultaneous equations y = -(x - 3) 2 + 2 and y = x 2 - 4x + 1.
    -(x - 3) 2 + 2 = x 2 - 4x + 1
    -2x 2 + 10 x - 8 = 0
    -x 2 + 5 x - 4 = 0
    Solutions: x = 1 and x = 4
    Use one of the equations to find y:
    x = 1 in the equation y = -(x - 3) 2 + 2 to obtain y = -(1 - 3) 2 + 2 = -2
    x = 4 in the equation y = -(x - 3) 2 + 2 to obtain y = -(4 - 3) 2 + 2 = 1
    Points: (1 , -2) and (4 , 1)
    Check answer graphically below.

    intersection of two parabolas



    • Example 6

  • Find the equation the parabola y = 2 x 2 + b x + c that passes by the points (-1,-5) and (2,10).


    Points (-1,-5) and (2,10) are on the graph of the parabola y = 2 x 2 + b x + c, hence.
    -5 = 2 (-1) 2 + b (-1) + c
    10 = 2 (2) 2 + b (2) + c
    Rewrite the above system in b and c in standard form.
    - b + c = - 7
    2 b + c = 2
    Solve the above system of equations to obtain: c = - 4 and b = 3
    Equation of the parabola that passes by the points (-1,-5) and (2,10) is: y = 2 x 2 + b x + c = 2 x 2 + 3 x - 4

    Use a graph plotter to check the answer by plotting the graphs of y = 2 x 2 + 3 x - 4 and check that the graph passes by the points (-1,-5) and (2,10).

    Example 7

  • Find the equation the parabola y = a x 2 + b x + c that passes by the points (0,3), (1,-4) and (-1,4).


    Points (0,3), (1,-4) and (-1,4) are on the graph of the parabola y = a x 2 + b x + c and are therefore solutions to the equation of the parabola. Hence we write the system of 3 equations as follows:
    3 = a (0) 2 + b (0) + c
    - 4 = a (1) 2 + b (1) + c
    4 = a (-1) 2 + b (-1) + c
    c = 3
    Substitute c by 3 in the last tow equations
    a + b = -7
    a - b = 1
    Solve the system in a and b
    a = - 3 and b = - 4
    Equation: y = a x 2 + b x + c = -3 x 2 - 4x + 3
    Plot the graphs of y = -3 x 2 - 4x + 3 and check that the graph passes through the points (0,3), (1,-4) and (-1,4).

    Example 8

    Question

    Question

    Example 9

    Question

    Example 10

    Question
    Question

    Question